07 Relational Database Design：Schema Normalization

这节课我是听的数据库第6章 关系数据理论（第二部分：范式理论 1NF-2NF-3NF） 也会有部分邓芳老师课程(英文部分)

范式理论

• 函数依赖
• 码
• 范式
• 2NF
• 3NF
• BCNF
• 多值依赖
• 4NF
• 规范化小结

范式级别表示的是这个范式的水平，级别越好，表示的越好 目标要求：

1. 判断是什么范式的表
2. 如何升级成更高范式的表

函数依赖

• 函数依赖的Def
• 平凡函数依赖与非平凡函数依赖
• 完全函数依赖与部分函数依赖
• 传递函数依赖

Def

定义：设R(U)是一个属性集上的关系模式，X和Y是U的子集。若对R(U)的任意一个可能的关系r（对表上的一行），r不可能存在两个元组在X上的属性值相等，而在Y的属性值不等，则称“X函数确定Y”或“Y函数依赖于X”，记作$X\to Y$。

1. 先找候选键
2. 再找主属性(候选键包含的属性)，区分主属性和非主属性

平凡/非平凡函数依赖

• $X\to Y,Y⊈X$则称$X\to Y$是非平凡的函数依赖
  • (Sno,Cno,Grade) $(Sno,Cno)\to Grade$
• $X\to Y,Y\subseteq X$则称$X\to Y$是平凡的函数依赖
  • $(Sno,Cno)\to Sno\to Cno$

若$X\to Y$，则X称为这个函数依赖的决定因素 若$X\to Y,Y\to X$，则记作$X\leftarrow \to Y$

完全函数依赖与部分函数依赖

Def:

在R(U)中，如果$X\to Y$，并且对于X的任何一个真子集X’,都有$X^{\prime }\nrightarrow Y$，则称Y对X完全函数依赖，记作$X\stackrel{F}{\to }Y$

若$X\to Y$，但Y不完全函数依赖于X，则称Y部分函数依赖于X，记作$X\stackrel{P}{\to }Y$

只需要X的部分属性(X的某个真子集)就能确定Y

题目中如何判断：

• 求出左边的真子集的闭包，看是否包含右边

传递函数依赖

Def:

在R(U)中，如果$X\to Y(Y⊈X),Y\nrightarrow X,Y\to Z,Z⊈Y$，则称Z对X传递函数依赖

Noted:如果$Y\to X,即X\leftarrow \to Y$，则Z直接依赖于X，而不是传递函数依赖

Keys and Functional Dependencies

Def:K is a superkey for relation schema R if and only if $K\to R$

Def:K is a candidate key for R if and only if

• $K\to R,and$
• for no $\alpha \subset K,\alpha \to R$（最小性）

DF allow constraints that cannt be expressed with superkeys.

范式

Def：符合某一种级别的关系模式的集合

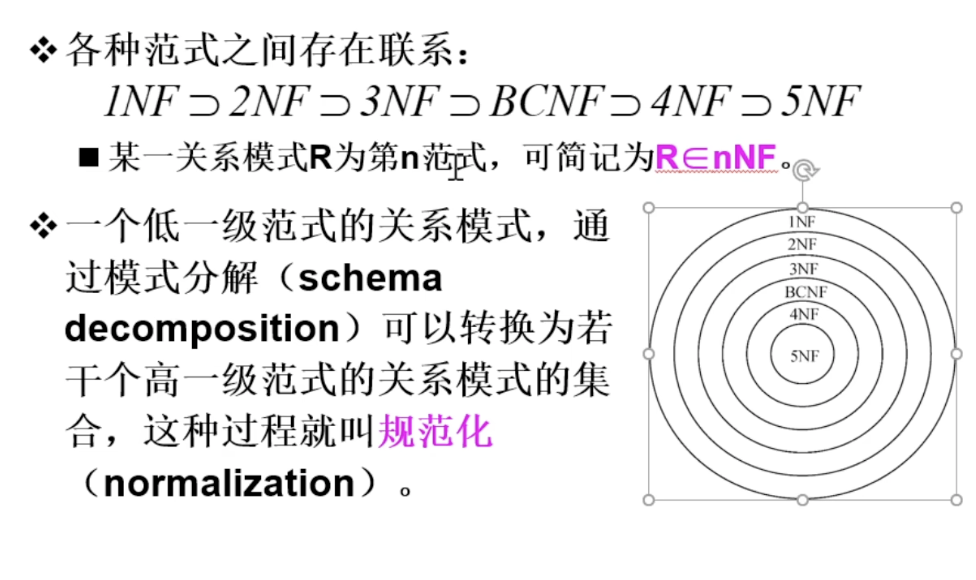1、2、3、BC范式是函数依赖 4、5NF是多值依赖 1NF：一个表中，每个格都是不可再细分的数据项

一个关系模式不属于3NF，会产生以下的问题：

数据冗余和增删改的异常

• 插入异常
  • 如果插入一个新学生，但该学生未选课，即该生无Cno，由于插入元组的时候必须给定主键，因此插入失败
• 删除异常
  • 如果S4只选了一门课C3，现在他不再选这门课，则删除C3后，整个元组的其他信息也被删除了
• 修改复杂
  • 如果一个学生选了多门课，则Sdept, Sloc被存储了多次。仍哦该生转系，需要修改所有相关的Sdept和Sloc，造成修改的复杂化

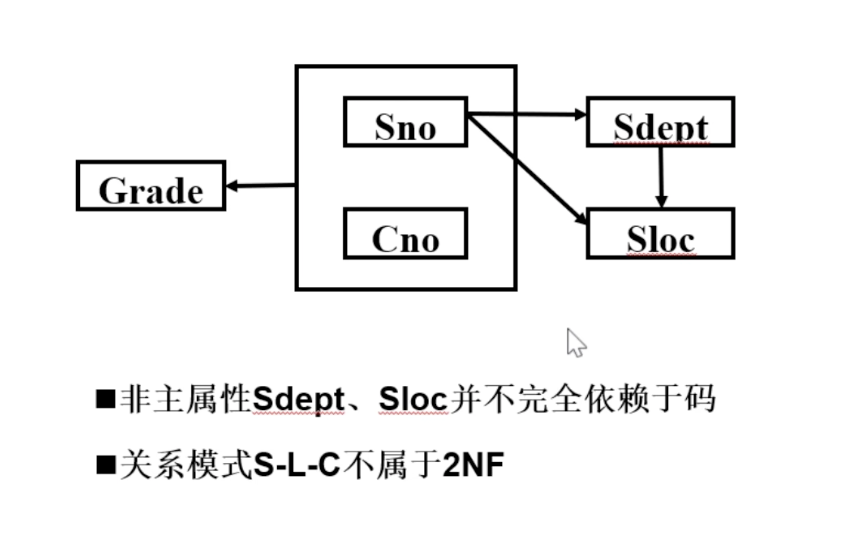
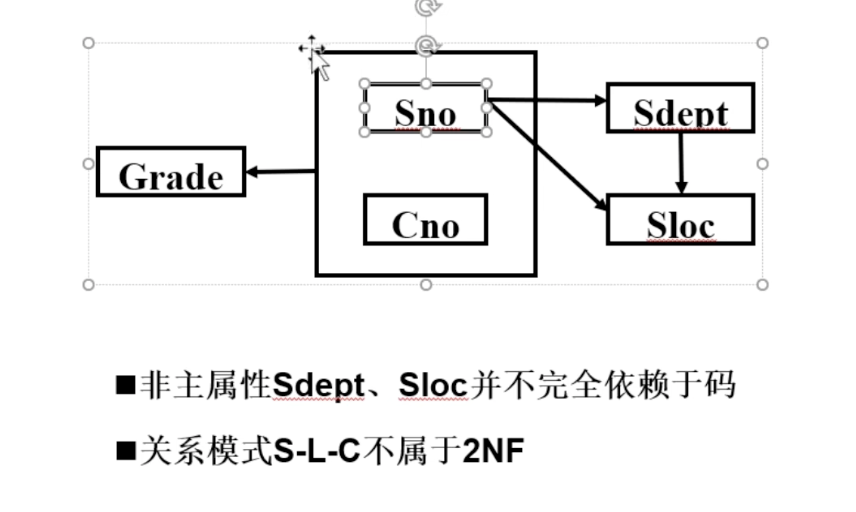
2NF

Def：若关系模式$R\in 1NF$，并且每个非主属性都完全函数依赖于任何一个候选键，则$R\in 2NF$

消除非主属性对主属性的部分函数依赖

即没有部分函数依赖

1. 找候选键，判断主属性和非主属性
2. 从主属性开始写，把所有的函数依赖关系列出来

如何升级为2NF

用投影分解把关系模式S-L-C分解为两个关系模式

“谁跟你好，复制自己，把他带走”

3NF

Def：设关系模式$R<U,F>\in 1NF$，若R中不存在这样的键X、属性组Y以及非主属性Z($Y⊈Z$)，使得$X\to Y,Y\to Z$成立，$Y\nrightarrow X$不成立，则称$R<U,F>\in 3NF$

非主属性对主属性没有传递函数依赖就是3NF

要求任意的一个函数依赖关系都要满足以下条件的一个

• 平凡依赖

• 左边是超键

• 右边是键属性

• SC没有传递依赖，因此$SC\in 3NF$

BCNF

• 除了平凡依赖，左边都要是超键

Def: 设关系模式$R<U,F>\in 1NF$，若$X\to Y$且$Y\subseteq X$时，X必含有键，则$R<U,F>\in BCNF$

数据依赖的公理体系

Armstrong’s Axioms

• reflexivity(自反律):$if\beta \subseteq \alpha ,then\alpha \to \beta$
• Augmentation(增广律):$if\alpha \to \beta ,then\gamma \alpha \to \gamma \beta$
• transitivity(传递律):$if\alpha \to \beta ,and\beta \to \gamma ,then\alpha \to \gamma$

可以得到三条推理规则

• 合并规则:$X\to Y,X\to Z\Rightarrow X\to YZ$
• 伪传递规则:$X\to Y,WY\to Z\Rightarrow XW\to Z$
• 分解规则:$X\to Y,Z\subseteq Y\Rightarrow X\to Z$

函数依赖集的闭包

• For R(U,F), The set of all functional dependencies logically implied by F is the closure of F.
  • E.g. If $A\to B$ and $B\to C$, then we can infer that $A\to C$
• We denote the closure of F by $F^{+}$

根据F能推导出来的所有函数依赖的集合，写了的+没写的

E.g.

$$U=\{A,B,C,D,E\},F=\{A\to B,B\to C,D\to E\}$$

则

$$F^{+}=\{A\to B,B\to C,D\to E,A\to C\}$$

这里的闭包求法其实在大二下的形式语言与自动机已经学过了

E.g.

已知关系模式$R<U,F>$，其中

$$\begin{array}{rl}& U=\{A,B,C,D,E\};\\ & F=\{AB\to C,BtoD,C\to E,EC\to B,AC\to B\}.\\ & 求(AB{)}_F^{\ast }\end{array}$$

Solution:

$$\begin{array}{rl}& X_0=\{AB\}\\ & X_1=X_0+CD=ABCD\\ & X_2=X_1+CDEB=ABCDE=U\\ & \\ & stop\end{array}$$

Conclusion:$AB\to U$,so $(AB{)}_F^{\ast }=U=ABCDE$

F的最小依赖集

Def：如果函数依赖集F满足下列条件，则称F为一个最小依赖集或者最小覆盖(离散数学下)

1. F中任一函数依赖的右部仅含有一个属性
   • E.g.$A\to BC\Rightarrow A\to B,A\to C$
2. F中不存在这样的函数依赖$X\to A$，使得F与$F-\{X\to A\}$等价
   • 不存在冗余的DF，先删除看看是否能推出
3. F中不存在这样的函数依赖$X\to A$，X有真子集Z使得$F-\{X\to A\}\cup \{Z\to A\}$与F等价
   • 留下最简单的

并非唯一

函数依赖集等价 Def:如果$G^{+}=F^{+}$，就说函数依赖集F覆盖G或F与G等价

两个函数依赖集等价是指他们的闭包等价

Decomposition(分解)

Decide whether a particular relation R is in “good” form.

All attributes of an original schema (R) must appear in the decomposition ($R_1,R,2,\dots ,R_n$):

$$R=R_1\cup R_2\cup \cdots \cup R_n$$

Lossless-join decomposition(无损连接的分解)

decompose R into a set of relations {$R_1,R_2\dots ,R_n$}, For all posisible relations r on schema R

$$r={\Pi }_{R_1}(r)\bowtie {\Pi }_{R_2}(r)\bowtie \cdots \bowtie {\Pi }_{R_n}(r)$$

A decomposition of R into $R_1$ and $R_2$ is lossless join if and only if at least one of the following dependencies is in $F^{+}$:

• $R_1\cap R_2\to R_1$
• $R_1\cap R_2\to R_2$

E.g.

$$\begin{array}{rl}& R=(A,B,C)\\ & F=\{A\to B,B\to C\}\\ & R_1=(A,B)\\ & R_2=(B,C)\end{array}$$

$R_1\cap R_2=\{B\}$ and $B^{+}=BC$

Dependency preservation(函数依赖保持)

decompose a relation schema R with a set of functional dependencies F into $R_1,R_2,\dots ,R_n$. Let $F_i$ be the set of dependencies $F^{+}$ that include only attributes in $R_i$

$$\begin{array}{rl}& (F_1\cup F_2\cup \cdots \cup F_n{)}^{+}=F^{+}\\ & F_i=\{X\to Y|X\to Y\in F^{+}\cap XY\subseteq R_i\}\end{array}$$

E.g.

$$\begin{array}{rl}& R=(A,B,C),F=\{A\to B,B\to C\}\\ & R_1=(A,B),R_2=(B,C)\end{array}$$

How to check if a dependency $\alpha \to \beta$ is preserved in a decomposition of R into $R_1,R_2,\dots ,R_n$

Code

result = $\alpha$ while (changes to result) do   for each $R_i$ in the decomposition     t = $(result\cap R_i{)}^{+}(F)\cap R_i$     $result=result\cup t$ if result contains all attributes in $\beta$, then the funcitonal dependency $\alpha \to \beta$ is preserved.

E.g.

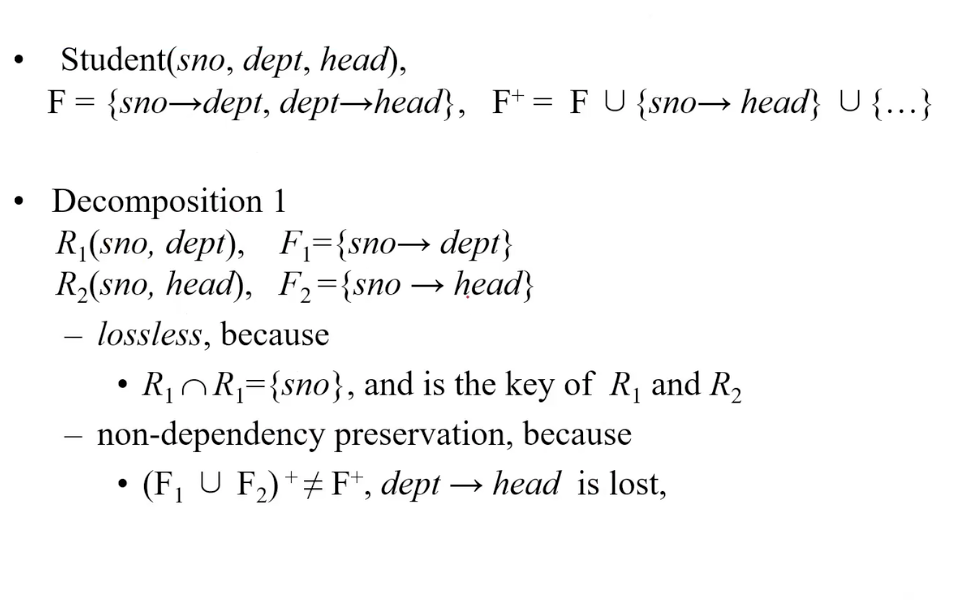
3NF Decomposition Algorithm

Code

Let $F_c$ be a canonical cover for F;(求F的最小函数依赖集$F_c$) i:=0 for each functional dependency $\alpha \to \beta$ in $F_c$ do if none of the schemas $R_j$, $1\le j\le i$ contains $\alpha \beta$ then begin i:=i+1; $R_i:=\alpha \beta$ end if none of the schemas $R_j,1\le j\le i$ contains a candidate key for R then begin $i:=i+1;$ $R_i:=anycancidatekeyforR;$ end $return(R_1,R_2,\dots ,R_n)$

1. 求F的最小函数依赖集$F_c$
2. 对于$F_c$的每个函数依赖关系，如果没有任何一个已经得到的关系模式包含$\alpha \beta$，则将其作为一个关系模式输出

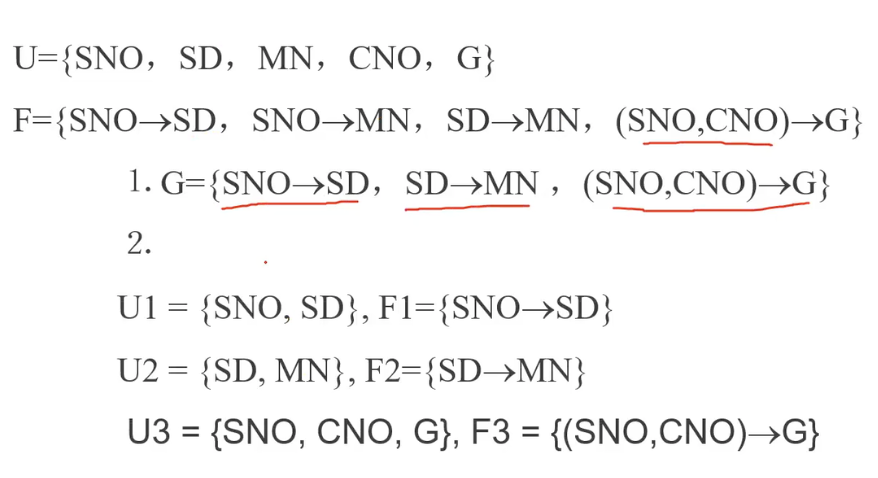Above algorithm ensures:

• each relation schema $R_i$ is in 3NF
• decomposition is dependency preserving
• decomposition is lossless-join

BCNF Decomposition Algorithm

Code

result:={R} done:=false compute $F^{+}$ while (not done) do if (there is a schema $R_i$ in result that is not in BCNF) then begin let $\alpha \to \beta$ be a notrivial functional dependency that holds on $R_i$, such that $\alpha dot\to R_i$ is not in $F^{+}$, and $\alpha \cap \beta =\varnothing$; result:={(result - $R_i$)$\cup$($R_i-\beta$)}$\cup${($\alpha ,\beta$)}; end else done:=true;

没有一个通用的方法去实现函数依赖保持，只有无损连接

但是针对特定的，可以考虑去实现